POST ON 2024-03-05 BY WOLVES

UPDATE ON 2024-10-05 BY WOLVES

Machine Learning

You can see the code of this blog on github

1.First chapter - instruction

1.1 supervised learning

• regression
• classification

1.2 unsupervised learing

• Clustering 聚类算法
• Dimensionality reduction
  • 少所考虑的随机变量数量的过程，目的是获得一组主要变量。

1.3 Jupyter Notebook

2.Supervised Learing

2.1 Linear regression

$$ f(x) = wx+b $$

• x is input feature / variable

A experiment:https://github.com/mohadeseh-ghafoori/Coursera-Machine-Learning-Specialization.git

• Cost function
  • Mean Squared Error, MSE - 均方差

$$ \text{Residual} = \hat{y}^{(i)} - y^{(i)} \ J(w,b) = \frac{1}{2m} \sum_{i=1}^{m} (y_{w,b}(x^{(i)}) - y^{(i)})^2 $$

• goal

$$ \underset{w,b}{minimize}\ J(w,b) $$

2.2 Gridient Descent

• 在当前的节点找下降速度最快的方向走一步，然后再找下一个方向，最终达到局部最小值loacl minima（贪心）

$$ w = w - \alpha\cdot\frac{\partial J(w,b)}{\partial w} $$

$$ b = b - \alpha\cdot\frac{\partial J(w,b)}{\partial b} $$

• $ \alpha $ is learning rate
• Simultaneously update
  • It mains we need calculate first , then update both of the value
• Here is negative gradient

Learning Rate

• Small
  • Gradient descent may be slow
• Large
  • Gradient descent may
    • Overshoot
    • Fail to converge
    • Diverge

Batch

• Each step of gradient descent

2.3 Multiple features (variables)

$$ \ {\vec{x}^{(2)}_{3}} = \begin{pmatrix}x_1 & x_2 & x_3 & x_4\end{pmatrix} $$

• $x_j = j^{th}$(feature)
• $n$ : number of features
• $\vec{x}^{(i)}$ : features of ($i^{th}$) training example
• $x_j^{(i)}$ : value of feature $j$ in ($i^{th}$) training example

2.3.1 Model

• Previously $$ f_{w,b}(x) = wx + b $$

• Now

  multiple linear regression $$ f_{w,b}(x) = w_1x_1 + w_2x_2 + \cdots + w_nx_n + b $$

  equals

  $$ \vec{w} = \begin{bmatrix} w_1 & w_2 & w_3 & \cdots & w_n \end{bmatrix} $$

  $$ \vec{x} = \begin{bmatrix} x_1 & x_2 & x_3 & \cdots & x_n \end{bmatrix} $$

  $$ f_{\vec{w} \cdot,b}(\vec{x}) = \vec{w} \cdot \vec{x} + b $$

  It is not moltivariate regression(多个自变量和因变量的关系，即矩阵和矩阵)

  $$ MSE = \frac{1}{2m} \sum_{i=1}^{m} (y_{w,b}(x^{(i)}) - y^{(i)})^2 $$

2.3.2 vectorization

• In python, we can use numpy to do the vectorization for accelerating the calculation.
• We oringally use for loop to do the calculation, but it is very slow, so we need to use vectorization to do the calculation.
• We will regard the vectorization as a matrix operation. Using matrix dot product to do the calculation.

2.3.3 Feature scaling

• our features have very different ranges, sometimes it will be very big or very small, so we need to scale them to the same range.

• In our second lab, we meet a problem that the result overflow, we can use a small learning rate to solve this problem, but it is not a good way. And now, Using feature scaling is a better way.

• After feature scaling, we can use a big learning rate to accelerate the convergence. This makes the linear regression more stable and faster than before. Additionally, feature scaling addresses the issue of features with different scales, which may cause the model to focus more on features with larger values and ignore those with smaller values. Moreover, it solves the problem of overflow.

• Standardization and Normalization

  • For example, $x \in [300, 2000]$ ,now we need to scale it to $[0, 1]$, we can use the formula $x' = \frac{x - \min(x)}{\max(x) - \min(x)}$

• Z-score

  • $x’ = \frac{x - \mu}{\sigma}$
  • $\mu$ is mean
  • $\sigma$ is standard deviation

2.3.4 Checking Convergence of Gradient Descent

• learning curve
  • use iteration number on the x-axis and cost on the y-axis
  • If the cost is decreasing, the gradient descent is working.
  • If the cost is not decreasing, the gradient descent is not working.

2.3.5 Feature Engineering

• Using intuition to design new features, by transforming or combining existing features.

2.3.6 Polynomial Regression

$$ f_{w,b}(x) = w_1x + w_2x^2 + w_3x^3 + b $$

• You will get a huge curve when x is very big, so we need to use feature scaling to solve this problem.

• In sklearn, We can use PolynomialFeatures to do the polynomial regression, and use Ridge regression or normal regression to do the regression.

  • Ridge (includes L2 regularization term) $$ \text{cost} = \frac{1}{2m} \sum_{i=1}^{m} (y_{w,b}(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^{n} w_j^2 $$
  • Normal $$ \text{cost} = \frac{1}{2m} \sum_{i=1}^{m} (y_{w,b}(x^{(i)}) - y^{(i)})^2 $$

classification

2.4 Logistic Regression

• Classification
• negative class != bad
  • 0
• positive class != good
  • 1
• We need to find a threshold to decide whether it is good or bad when we use normal linear regression.
• logistic regression is a curve, not a straight line and it needs a threshold too.
• sigmoid function $$ z = \vec{w} \cdot \vec{x} + b $$

$$ g(z) = \frac{1}{1 + e^{-z}} $$

$$ \therefore f_{\vec{w},b}(x) = g(z) = \frac{1}{1 + e^{-(\vec{w} \cdot \vec{x} + b)}} $$

• decision boundary

  • the boundary of the classification
  • the boundary of the logistic regression is a straight line for two features
  • the boundary`s function is $f_{\vec{w},b}(x) = 0.5$ , when $f_{\vec{w},b}(x) \geq 0.5$ , it is positive class, otherwise it is negative class. Therefore, z = 0 is the boundary.

• non-linear decision boundary

  • the boundary of the classification is a curve
  • the fuction is not a straight line

• It not a convex function, so it not a good way to use gradient descent to find the minimum.

  • So MSE is called the loss on a single training example in this case.

• cost function - maximum likelihood function

$$ \text{cost}(f_{\vec{w},b}(x),y) = \begin{cases} - \ln(f_{\vec{w},b}(x)) & \text{if } y = 1 \\ - \ln(1 - f_{\vec{w},b}(x)) & \text{if } y = 0 \end{cases} $$

As f is a sigmoid function, so $0 \leq f_{\vec{w},b}(x) \leq 1$, so the cost function is a convex function.

$$ J(\vec{w},b) = \frac{1}{m} \sum_{i=1}^{m}\text{cost}(f_{\vec{w},b}(x^{(i)}),y^{(i)}) = \begin{cases} - \ln(f_{\vec{w},b}(x^{(i)})) & \text{if } y^{(i)} = 1 \\ - \ln(1 - f_{\vec{w},b}(x^{(i)})) & \text{if } y^{(i)} = 0 \end{cases} $$

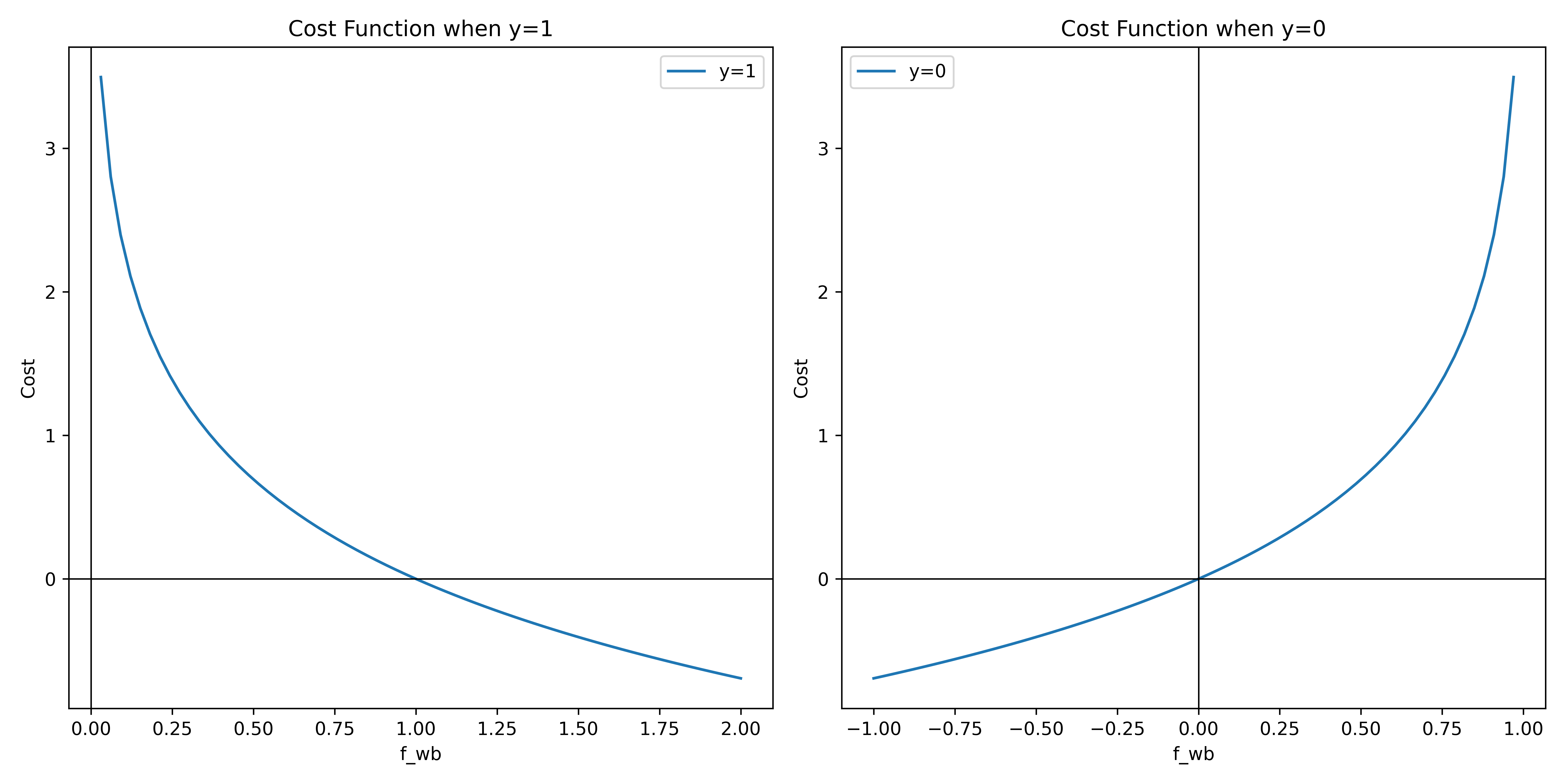
• simple cost function
  • Binary Cross-Entropy Loss Function (二分类交叉熵损失函数)

$$ \text{cost}(f_{\vec{w},b}(x^{(i)}),y^{(i)}) = -y^{(i)}\ln(f_{\vec{w},b}(x^{(i)})) - (1-y^{(i)})\ln(1-f_{\vec{w},b}(x^{(i)})) $$

$$ J(\vec{w},b) = -\frac{1}{m} \sum_{i=1}^{m} \left( y^{(i)}\ln(f_{\vec{w},b}(x^{(i)})) + (1-y^{(i)})\ln(1-f_{\vec{w},b}(x^{(i)})) \right) $$

$$ \frac{\partial J(\vec{w},b)}{\partial w_j} = \frac{1}{m} \sum_{i=1}^{m} (f_{\vec{w},b}(x^{(i)}) - y^{(i)})x_j^{(i)} $$

$$ \frac{\partial J(\vec{w},b)}{\partial b} = \frac{1}{m} \sum_{i=1}^{m} (f_{\vec{w},b}(x^{(i)}) - y^{(i)}) $$